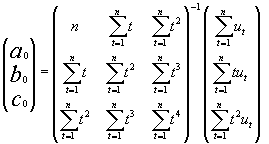Matemáticas. Axuste linear e parabólico polo método de mínimos cadradados
Índice
Axuste linear polo método de mínimos cadrados
Neste apartado trataremos de explicar como axustar as observacións dunha variable U1, U2, ..., Un a unha recta (a+bt).
O método de mínimos cadrados consiste en encontrar os parámetros a0 e b0 que minimicen a suma dos cuadrados dos residuos. É dicir, hai que atopar a0 e b0 de forma que fagan mínima f(a,b) = St (ut - (a+b·t))2.
O que debemos facer é calcular as derivadas parciais respecto a a e b e igualalas a cero:
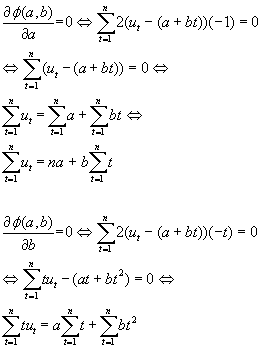
Entón obteríamos o seguinte sistema de ecuacións
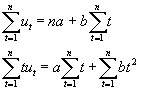
que expresada de forma matricial quedaríanos do seguinte xeito
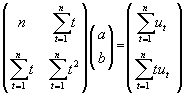
Polo tanto:
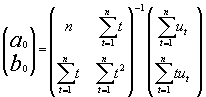
Axuste parabólico polo método de mínimos cadrados
Para calcular o axuste parabólico (a+bt+ct2) hai que minimizar a seguinte función:
f(a,b,c) = St (ut - (a+b·t+c2))2.
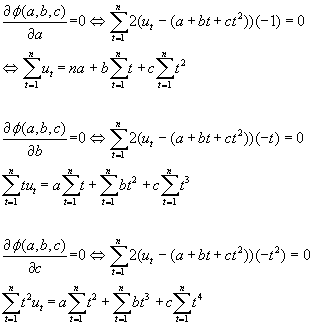
Teríamos, por tanto, que resolver:
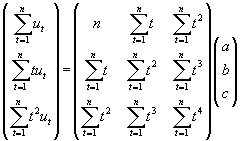
Por tanto, os parámetros a0, b0 e c0 da parábola que axusta a serie de datos U1, U2, ..., Un, ven dada por: