Matemáticas. Regresión
Definicións e conceptos teóricos

Correlación. Diagrama de dispersión

Correlación

Unha variable bidimensional (X,Y) é o resultado de observar en cada individuo dunha poboación ou mostra dúas características ou variables estatísticas, X e Y.

Exemplo:

(X,Y)=("Idade media da poboación","Renda dispoñible bruta por habitante") nos 315 concellos galegos

As dúas variables que interveñen nunha variable bidimensional poden estar relacionadas. Agora ben, cómpre sinalar que cando traballemos con variables estatísticas as relacións non son, en xeral, funcionais, senón que serán relacións máis difusas que non se poderán expresar a través dunha función.

Recorda que...

...sempre que queramos falar da relación ou dependencia entre dúas variables falaremos de correlación entre ambas as dúas variables.

¿Como se pode clasificar a correlación entre dúas variables?

• Correlación lineal ou non lineal: a correlación entre dúas variables é lineal se a nube de puntos se concentra en torno a unha recta. Pola contra, é non lineal cando a nube de puntos se axusta a unha función non lineal.

• Correlación positiva ou negativa (ou ben directa ou inversa): a correlación é positiva (directa) cando a medida que unha das variables crece a outra tamén crece. Pola contra é negativa cando ao aumentar unha das variables a outra diminúe.

• Correlación de tipo funcional: cando a correlación entre dúas variables pode describirse a través dunha certa función.

Diagrama de dispersión ou nube de puntos

Un primeiro indicador visual da existencia de correlación entre dúas variables é a nube de puntos ou diagrama de dispersión, que consiste nun sistema de eixos coordenados que representan os posibles valores de cada variable, no que se reflicten os distintos pares de puntos observados. Estes diagramas son moi útiles para indicarnos se existe ou non relación entre as dúas variables e medir o sentido e a intensidade da dita relación.

Exemplo:

Consideramos a variable bidimensional (X,Y) onde X="idade media da poboación" e Y="renda dispoñible bruta en euros por habitante" nos 315 concellos galegos no ano 2009. Nas seguintes ligazóns están dispoñibles o datos empregados: idade media da poboación , renda dispoñible bruta por habitante

¿Existe relación entre ambas as dúas variables?

Para investigar a existencia de correlación entre as variables realizamos en primeiro lugar o gráfico de dispersión.

A nube de puntos permite observar como a medida que se incrementa a idade media da poboación diminúe a renda dispoñible bruta por habitante, polo que estariamos ante unha correlación inversa.

Covarianza

A covarianza é unha medida que permite cuantificar a variabilidade conxunta das variables X e Y. Calcúlase como a media aritmética dos produtos das desviacións de cada variable respecto da media.

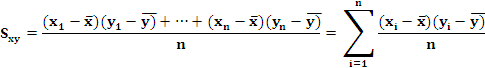
O signo da covarianza permite coñecer como interactúan as variables:

Se Sxy>0, ao aumentar os valores de X aumentan os de Y e dise que hai unha relación directa entre as variables
Se Sxy<0, ao aumentar os valores de X diminúen os de Y e dise que hai unha relación inversa entre as variables
Se Sxy=0, as variables están incorreladas, non hai relación lineal entre as variables, pero isto non significa que non teñan relación estatística

¿Pode empregarse a covarianza para medir se a correlación lineal entre dúas variables e forte o débil?

¡¡¡NON!!! A covarianza é sensible á escala de medida polo que o seu valor depende das unidades nas que se expresen as variables.

Exemplo:

Poderiamos calcular agora a covarianza entre a idade media da poboación e a renda dispoñible bruta por habitante. A nube de puntos entre estas dúas variables é descendente, polo tanto xa sabemos de antemán que a covarianza terá signo negativo.

O valor da covarianza entre estas dúas variables é:

S_xy = -5.597,6

Coeficiente de correlación

Cando a nube de puntos dunha variable bidimensional se concentra en torno a unha recta existe unha correlación de tipo lineal. Nestes casos, necesítase unha medida que permita cuantificar esa relación.

O coeficiente de correlación lineal de Pearson defínese como:

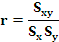
onde S_xy é a covarianza de X e Y, S_x a desviación típica de X e S_y a desviación típica de Y.

O signo do coeficiente de correlación está determinado polo signo da covarianza, posto que as desviacións típicas son sempre positivas.

Ademais, a diferenza da covarianza, ¡¡non varía cos cambios de escala!!, polo que permite non só interpretar o sentido da correlación (directa ou inversa) senón tamén a súa magnitude (forte ou débil).

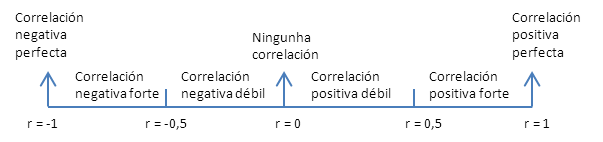
O coeficiente de correlación proporciona, polo tanto, información sobre o tipo de correlación que existe entre as variables X e Y:

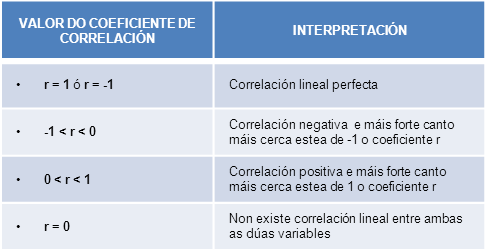
Exemplo:

Calculamos agora o coeficiente de correlación lineal entre as variables idade media da poboación e a renda dispoñible bruta por habitante. Para calculalo precisamos coñecer os valores da covarianza entre as dúas variables, e a desviación típica de cada unha delas.

Temos que:

S_xy = -5.597,6

S_x = 5,3

S_y = 2117,6

Polo tanto:

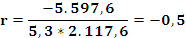
e estariamos nun caso de correlación lineal negativa moderada.

Recta de regresión

Nalgúns casos, cando representamos a nube de puntos dunha variable bidimensional, observamos que se parece á gráfica dalgunha das curvas coñecidas. De todas as curvas que se aproximan, a que "mellor" se aproxima á nube de puntos, é dicir, con maior exactitude, denomínase curva de regresión.

A función que mellor se aproxima á nube de puntos pode ser lineal, de segundo grao, exponencial, logarítmica, ... Cando a función é lineal a curva de regresión denomínase recta de regresión.

¿Cando axustaremos unha nube de puntos por unha recta?

O axuste da nube de puntos por unha recta só debe de facerse cando existe correlación lineal entre ambas as dúas variables.

Para determinar a recta de regresión (y = a + bx), é dicir, a recta que con maior exactitude se aproxima á nube de puntos, emprégase o método de mínimos cadrados.

Cada punto x_i da variable X terá:

• Por unha parte, o valor correspondente á variable Y, y_i
• Por outra, a súa imaxe pola recta de regresión y = a+ bx_i

Entre estos dous valores existirá unha diferenza:

d_i = y_i - a - bx_i

Mediante o método de mínimos cuadrados obtense a recta que fai mínima a suma dos cadrados de todas estas diferenzas.

Recta de regresión de Y sobre X

A ecuación da recta de regresión de Y sobre X que se obtén mediante o método de mínimos cadrados é a seguinte:

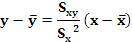
Observa que:

• A recta pasa polo centro de gravidade da nube de puntos.

• O signo da pendente da recta de regresión é o da covarianza. Se é positivo a recta é ascendente (pendente positiva); se é negativo, descendente (pendente negativa).

Se queremos expresar a recta da forma y = a + bx, entón, os parámetos a e b obtéñense a partir das seguintes expresións:

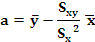
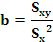
Exemplo:

Calculamos agora a recta de regresión da variable Y="renda dispoñible bruta en euros por habitante" sobre X="idade media da poboación".

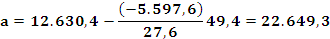
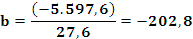
¿Que utilidade ten a recta de regresión?

O coñecemento da recta de regresión permite obter os valores dunha variable (neste caso Y) a partir de valores coñecidos da outra variable (X). Os valores de Y obtidos sustituíndo na ecuación da recta valores coñecidos de X denomínanse valores esperados.

Exemplo:

A recta de regresión da renda dispoñible bruta por habitante sobre a idade media da poboación pódese empregar para facer estimacións.

Podemos obter valores esperados do índice de envellecemento (Y) a partir de valores coñecidos da idade media da poboación (X).

Na seguinte táboa móstrase a idade media da poboación nos concellos da Coruña e de Santiago:

¿Cal é o valor esperado da renda dispoñible bruta por habitante neses concellos?

O valor esperado da renda dispoñible bruta por habitante no concello da Coruña é:

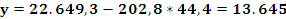
O valor esperado da renda dispoñible bruta por habitante no concello de Santiago de Compostela é: