Portal educativo IGE


ver o mapa do portal

Matemáticas. Regresión
Actividade 4: poboación menor de 16 anos e número de pediatras en atención primaria

FICHA DA ACTIVIDADE

Obxectivos

  • Familiarizar ao estudante cos datos de poboación e recursos a nivel comarcal
  • Interpretación dun gráfico de dispersión
  • Analizar a dependencia entre dúas variables: covarianza e coeficiente de correlación
  • Cálculo da recta de regresión
  • Utilización da recta de regresión para predicir

Palabras clave

  • Comarca
    Territorio natural que abrangue concellos e vilas con características xeográficas, económicas e culturais comúns.

Coñecementos previos necesarios

  • Coñecementos básicos de estatística
  • Saber confeccionar e interpretar gráficos

Cuestións a resolver:

Coa información que se facilita nos enlaces e mediante cálculos sinxelos que se desenvolven nesta actividade, poderás responder ás seguintes preguntas:

  1. ¿Cantos pediatras ten asignados a túa comarca?.....................................E, ¿canta poboación menor de 16 anos reside nela?..........................................
  2. ¿Cales son as comarcas nas que reside menos poboación menor de 16 anos?................................................................... ¿Estas comarcas son as que teñen menos pediatras en atención primaria?.................................................................................
  3. ¿Existe algún tipo de relación entre a poboación menor de 16 anos e o número de pediatras?..................................................... De existir relación, ¿poderíase dicir que é unha relación lineal positiva? Xustifica a túa resposta cunha medida estatística...............................................................................................................................................................................
  4. ¿Cal é a pendente da recta que mellor axusta a nube de puntos?................................................................................................
  5. ¿Poderías empregar a recta de regresión para predicir os valores dos pediatras que lle corresponderían ás comarcas que faltan?.......................................... ¿Que indica o signo do erro de predición?............................................................................

Descarga de datos

Descarga da ficha en pdf

Índice

Poboación menor de 16 anos e número de pediatras por comarca


Un bó comezo para coñecer como se distribúen o número de pediatras nas comarcas galegas é facer un mapa no que se represente a variable:

Mapa 1: Distribución do número de pediatras nas comarcas de Galicia

No mapa pódese observar que as comarcas con maior número de pediatras en atención primaria son nas que se atopan as grandes cidades como A Coruña, Ferrol, Santiago, Lugo, Ourense, Vigo e Pontevedra, e unha serie de comarcas costeiras como O Morrazo, O Salnés, Barbanza e Bergantiños onde o número de pediatras é maior ou igual a 9.

¿Poderíase dicir que os recursos (pediatras) están ben repartidos? Ao facer o mapa da distribución dos menores de 16 anos pode verse que as comarcas con maior número de menores de 16 anos coindiden coas comarcas con maior número de pediatras:

Mapa 2: Distribución dos menores de 16 anos nas comarcas de Galicia

A información que se amosa nos mapas indica que as dúas variables distribúense de manerira similar nas comarcas galegas, é dicir, as comarcas que teñen un maior número de rapaces menores de 16 anos teñen maior número de pediatras e aquelas nas que hai menos poboación nova, como Terra de Trives ou Terra de Caldelas, teñen menos pediatras en atención primaria.

Esta primeira análise gráfica xa permite intuír que entre as dúas variables pode existir unha relación, e de existir, esta relación será directa ou positiva, a máis poboación menor de 16 anos maior número de pediatras.

¿Existe algún tipo de relación entre a poboación menor de 16 ano e o número de pediatras?

Nas táboas seguintes móstranse os datos de poboación e número de pediatras para as comarcas galegas no ano 2012, excluídas as comarcas da Coruña e Vigo.

Para representar graficamente os datos empregaremos o "diagrama de dispersión", que permite representar nos eixos coordenados os pares de puntos formados polos valores observados de ambas as dúas variables.

No eixo de ordenadas representamos a variable explicada (tamén chamada endóxena ou dependente), que neste caso é o número de pediatras, e no eixo de abscisas a variable explicativa (esóxena ou independente), que é a poboación menor de 16 anos.

O gráfico de dispersión do número de pediatras e a poboación menor de 16 anos das 51 comarcas consideradas é:

No gráfico apréciase que ao aumentar os valores da variable independente (poboación menor de 16 anos), aumenta o valor da variable dependente (número de pediatras nesa comarca), ou o que é o mesmo, que as comarcas con máis poboación menor de 16 anos teñen tamén un maior número de pediatras asignados, confirmando así que a relación entre as dúas variables é directa ou positiva como xa se podía ver nas distribucións xeográficas das variables.

¿Que medida se debe empregar para identificar e cuantificar a dependencia entre as dúas varibles?

Primeiro, para medir a asociación lineal entre dúas variables calcúlase a covarianza, cuxa fórmula matemática é:

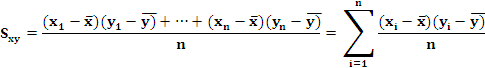
A covarianza entre a poboación menor de 16 anos e o número de pediatras toma o valor 30.305,03. Ao ser distinta de 0 pódese dicir que en principio hai certa dependencia lineal. Ademais, o signo da covarianza, positivo neste caso, determina o sentido da correlación.

Outra forma de identificar o sentido da correlación é calcular o centro de gravidade da nube puntos 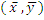e trazar uns novos eixos coordenados por ese punto; se a maioría dos puntos están no primeiro e terceiro cuadrante moitos produtos 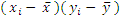son positivos e a covarianza é positiva, e se a maioría están no segundo e cuarto cuadrante será negativa.

O centro de gravidade da nube de puntos calcúlase como a media da variable x e a media da variable y, que neste caso é o punto:

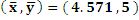
No gráfico vese que os puntos sitúanse no primeiro e terceiro cuadrante, o que confirma que a dependencia lineal é positiva como xa se veu co signo da covarianza.

Para cuantificar a relación entre as dúas variables emprégase o coeficiente de correlación lineal de Pearson, cuxa expresión matemática é:

que neste caso toma o valor r = 0,986.

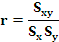
¡¡¡O coeficiente de correlación está moi próximo a 1 o que indica que a relación é forte e directa!!!

¿Que recta é a que mellor axusta a nube de puntos?


Como o valor do coeficiente de correlación lineal indica unha relación lineal moi forte, pódese tratar de axustar a nube de puntos mediante unha recta. Chámase recta de regresión á recta que describe como varía a media da variable dependente en función da independente e é a que mellor axusta a nube de puntos.

A recta de regresión presenta a seguinte ecuación y= a + bx, onde os valores dos parámetros a e b obtéñense mediante o método de mínimos cadrados, é dicir, mediante as seguintes expresións:

      

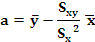
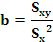
e, polo tanto, a expresión da recta que mellor axusta a nube de puntos xerada pola variable bidimensional, poboación menor de 16 anos e número de pediatras en atención primaria, é:

y = 0,294 + 0,001 x

Por outra banda, unha recta queda definida de forma única mediante un punto da recta e a pendente desta. A pendente da recta de regresión correspóndese co coeficiente b obtido mediante mínimos cadrados e como punto pódese tomar o centro de gravidade da nube de puntos xa que sempre pertence á recta de regresión. Así, a recta de regresión pódese expresar mediante:

Punto: ( 4.571 , 5 )  e  Pendente: 0,001

No seguinte gráfico representamos a recta de regresión xunto co diagrama de dispersión:

¿Cantos pediatras lle corresponden segundo a recta ás comarcas de A Coruña e Vigo?

A ecuación da recta de regresión relaciona ambas as dúas variables (a poboación menor de 16 anos e o número de pediatras) e ao coñecer a poboación menor de 16 anos dunha comarca poderase calcular o número de pediatras que lle corresponden segundo a recta de regresión.

Na táboa seguinte móstrase a poboación menor de 16 anos das comarcas da Coruña e Vigo:

Comarca Poboación menor de 16 anos
A Coruña 53.982
Vigo 60.267

Substituíndo na recta de regresión obtéñense as seguintes predicións do número de pediatras:

No caso da comarca da Coruña terase:

Pediatras preditos = 0,294 + 0,001 * (Poboación menor de 16 anos) = 0,294 + 0,001 * 53.982 = 54

Comarca Poboación menor de 16 anos Pediatras preditos
A Coruña 53.982 54
Vigo 60.267 61

¿Cal é o residuo ou erro de predición cometido ao utilizar a recta de regresión?

Ao facer unha estimación, neste caso mediante a recta de regresión, sempre se comente un erro. Este erro calcúlase como:

erro de predición=valor observado-valor esperado

Tendo en conta que no ano 2012 o número de pediatras na comarca de A Coruña é 47, o erro de precidión da dita comarca é -7 pediatras. Así, pódese construír a seguinte táboa:

Comarca Poboación menor de 16 anos Pediatras preditos Pediatras observados Erro
A Coruña 53.982 54 47 -7
Vigo 60.267 61 53 -8

En ambos os dous casos o erro de predición ten signo negativo, o que indica que a recta de regresión estima valores máis elevados dos reais para estas comarcas.

Podes contestar ás preguntas formuladas na actividade cos datos das comarcas da túa provincia, que podes atopar na ligazón que aparece ao principio desta páxina.

Ademais, podes seleccionar todas as comarcas de Galicia, incluídas as de A Coruña e Vigo, e construír a recta de regresión:

  • ¿Varía moito a relación entre as dúas variables?¿Están máis correladas que antes ou menos?¿Como o sabes?
  • ¿Que explicación lle podes dar a que as rectas de regresión teñan a mesma pendente?