Portal educativo IGE


ver o mapa do portal

Matemáticas. Regresión
Actividade 2: renda dispoñible bruta por habitante e idade media nos concellos galegos

FICHA DA ACTIVIDADE

Obxectivos

  • Interpretación dun gráfico de dispersión
  • Analizar a dependencia entre dúas variables
  • Obtención do coeficiente de correlación como medida da relación lineal
  • Cálculo da recta de regresión

Palabras clave

  • Renda dispoñible bruta por habitante
    Esta macromagnitude mide os ingresos de que dispoñen os fogares ao longo dun ano para destinar a consumo ou aforro e reflicte a capacidade adquisitiva dos fogares como resultado dos procesos de produción, asignación e distribución da renda.
  • Idade media no 1 de xaneiro
    Calcúlase como a media aritmética das idades dos individuos da poboación

Coñecementos previos necesarios

  • Coñecementos básicos de estatística
  • Saber confeccionar e interpretar gráficos

Cuestións a resolver:

Coa información que se facilita nos enlaces e mediante cálculos sinxelos que se desenvolven nesta actividade, poderás responder ás seguintes preguntas:

  1. ¿Cal é a renda bruta dispoñible por habitante e a idade media da túa provincia?..................... ¿E a do teu concello?......................
  2. ¿Poderías dicir que na túa provincia as variables renda dispoñible bruta por habitante e idade media da poboación están relacionadas?.........................¿Que tipo de relación atopas?.................. ¿É positiva ou negativa?.........................
  3. ¿O coeficiente de correlación lineal de Pearson confirma as túas sospeitas sobre a relación entre as dúas variables? ........................................................
  4. ¿Cales son os coeficientes a e b da recta de regresión que representa a relación entre a renda bruta dispoñible por habitante e a idade media? .................................................................................................... ¿A pendente da recta é maior ou menor que a da calculada para a provincia de Pontevedra? ..............................

Descarga de datos

Descarga da ficha en pdf

Índice

Distribución conxunta das variables renda dispoñible bruta por habitante e idade media da poboación


A renda dispoñible bruta do sector fogares é a variable que mellor reflicte o nivel de renda das familias residentes nun determinado territorio económico. Esta macromagnitude mide os ingresos de que dispoñen os fogares ao longo dun ano para destinar ao consumo ou ao aforro e reflicte a capacidade adquisitiva dos fogares como resultado dos procesos de produción, asignación e distribución da renda.

Por outra banda, a idade media da poboación informa sobre o grao de envellecemento do concello. Así, nos concellos con moita xente nova, en idade de traballar e xerar renda, a idade media da poboación será menor que nos concellos onde hai máis xente maior, que polo xeral recibe prestacións.

Na Táboa 1 móstranse os datos da renda bruta dispoñible por habitante e da idade media para 60 concellos da provincia de Pontevedra no ano 2017 (o concello de Cerdedo-Cotobade non ten dato dispoñible).

Táboa 1: Renda bruta dispoñible por habitante e idade media dos concellos da provincia de Pontevedra

A consideración da distribución conxunta das dúas variables permitirá estudar se existe algún tipo de relación entre elas.

¿Existe algún tipo de relación entre as dúas variables?


O primeiro paso para saber se existe algún tipo de relación entre as dúas variables que estamos estudando é representar a nube de puntos.

¿Como? Pintamos no plano cartesiano os puntos determinados polos pares de valores da táboa anterior.

E, ¿que variable escollemos para cada eixo?

O mellor é representar no eixo de ordenadas (Y) a variable explicada (tamén chamada endóxena ou dependente) e no eixo de abscisas (X) a variable explicativa (esóxena ou independente).

No noso caso o máis lóxico é pensar que a renda dispoñible bruta por habitante de cada concello depende da idade media do concello, así que a nosa variable explicada é a renda dispoñible bruta e a nosa variable explicativa é a idade media:

Idade media    Variable explicativa    Eixo X
Renda dispoñible bruta por habitante    Variable explicada    Eixo Y

Así obtemos o seguinte gráfico de dispersión:


¿Que conclusións podemos deducir do gráfico de dispersión?

Se observamos o gráfico podemos apreciar que ao aumentar os valores da variable independente (representada no eixo das x), diminúe en promedio o valor da variable dependente (representada no eixo das y). Cando esto ocorre dicimos que existe unha relación negativa ou inversa entre ambas variables.

Variable independente      Variable dependente    ¡¡¡ relación negativa !!!!

Efectivamente, o gráfico mostra que os concellos con alta idade media tenden a ter unha renda dispoñible bruta por habitante menor, confirmando así o que sospeitabamos ¿non si?

¿Poderiamos dicir que existe relación entre as dúas variables? ¿De que tipo?

A nube de puntos representada no gráfico de dispersión semella agruparse arredor dunha línea recta imaxinaria, esto quere dicir que a relación é lineal pero debemos ter en conta que os puntos non se sitúan exactamente nunha recta polo que a relación é de tipo estatístico e non funcional.

¿ Existe algunha forma de resumir numericamente a información contida no gráfico de dispersión?


A covarianza dá información sobre a asociación lineal entre dúas variables. ¡¡Coidado!!, mide a asociación lineal, non proporciona ningunha información se a relación é doutro tipo.

No noso caso temos:

De aquí, podemos deducir que hai certa dependencia lineal (se non a houbese a covarianza sería 0), e que esta é negativa pois o signo da covarianza tamén o é. Pero xa non deducimos nada máis, non podemos saber se a relación é forte ou non.

¿Por que? ¡¡¡¡ A covarianza non é unha medida adimensional !!!!!, depende das unidades de medida, polo que non hai uns límites a partir dos que se poida considerar que a relación sexa máis ou menos lineal.

¿Como se soluciona esto?

Para construír unha medida da relación lineal entre dúas variables, que resuma a información do gráfico de dispersión e que non dependa das unidades de medida, a solución proposta por Galton e Pearson foi tipificar a covarianza dividíndoa polas desviacións típicas de ambas as dúas variables. O resultado chámase coeficiente de correlación lineal de Pearson. Se o calculamos, no noso caso temos:

O coeficiente de correlación é sempre un valor entre -1 e 1. Ten o signo da covarianza, será positivo en relacións positivas (ou directas) e negativo en relacións negativas (ou inversas). Asimesmo, ao igual ca covarianza, é 0 cando non existe relación lineal, pero de novo ¡coidado!, pois só mide relacións lineais e podería ser cero cando exista unha relación moi forte entre dúas variables pero de tipo non lineal.

Cando as variables estean relacionadas linealmente de forma exacta, o coeficiente de correlación será igual a 1 en valor absoluto. Polo tanto, canto máis forte sexa a relación lineal entre as variables máis preto (en valor absoluto) estará de 1 o coeficiente de correlación lineal. 

No noso exemplo, o coeficiente de correlación é - 0,73. Polo tanto, hai motivos para pensar nunha certa relación lineal negativa.

Nota: todos os cálculos das operacións están realizados con todos os decimais resultantes, aínda que só se representen dous decimais nas fórmulas desta actividade.

¿Como construímos a recta de regresión ?


Agora axustaremos unha liña recta ao diagrama de dispersión. A recta de regresión é a recta que describe como varía a media da variable dependente en función da independente.

Como xa sabes, a ecuación dunha recta é da forma:

y = a + b x

Trátase agora de atopar os coeficientes a e b. Se definimos o erro de predición como:

erro de predición=valor observado - valor previsto

interésanos atopar a recta que conduza a menor erro . Para elo construimos unha medida agregada de canto difiren os valores preditos das yi respecto aos valores reais, a suma de erros ao cadrado.

Utilizando métodos matemáticos que non imos explicar agora, obtemos os coeficientes da recta que minimizan a expresión anterior e que son:

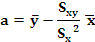
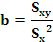
Imos ver como sería no noso exemplo:

polo tanto a nosa recta é:

y = 28.239,5 - 340,96 x

Xa temos a fórmula da recta de regresión.

Agora representámola graficamente enriba do diagrama de dispersión e obtemos o seguinte gráfico:


Actividades:

Podes contestar ás preguntas formuladas na actividade cos datos da túa provincia e cos de toda Galicia, que podes atopar na ligazón que aparece ao principio desta páxina.

A partir dos datos da túa provincia debes xerar o diagrama de dispersión para respostar ás seguintes preguntas:

  • ¿Existe dependencia entre estas variables?
  • ¿Que tipo de dependencia e de que signo?
E logo, poderás construír, como fixemos na actividade, a recta de regresión a partir dos coeficientes a e b.