
Matemáticas. Regresión
Actividade 1: taxa bruta de mortalidade e índice de envellecemento
FICHA DA ACTIVIDADE
Obxectivos
- Familiarizar ao estudante cos indicadores demográficos
- Interpretación dun gráfico de dispersión
- Analizar a dependencia entre dúas variables
- Obtención do coeficiente de correlación como medida da relación lineal
- Cálculo da recta de regresión
- Utilización da recta de regresión para predicir
Palabras clave
- Taxa bruta de mortalidade
A taxa bruta de mortalidade é o número de defuncións por cada 1.000 habitantes - Índice de envellecemento
O índice de envellecemento é a relación entre a poboación maior de 64 anos e a poboación menor de 20 anos:
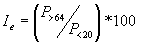
Coñecementos previos necesarios
- Coñecementos básicos de estatística
- Saber confeccionar e interpretar gráficos
Cuestións a resolver:
Coa información que se facilita nos enlaces e mediante cálculos sinxelos que se desenvolven nesta actividade, poderás responder ás seguintes preguntas:
- ¿Cal é a taxa bruta de mortalidade de Galicia?..........................................¿E a do teu concello?..........................................
- ¿Cales son os concellos da túa provincia con menor índice de envellecemento?..........................................¿Morre menos xente alí?..........................................
- ¿Existe unha relación directa entre o índice de envellecemento e a taxa bruta de mortalidade? É dicir, ¿morre máis xente nos concellos con maior índice de envellecemento?..........................................
- ¿Pódese establecer unha relación lineal entre as dúas variables?..........................................
- Se che falta o dato dun concello, ¿poderías utlizar a recta de regresión para predecilo?..........................................
Descarga de datos
- Os datos do ano 2023 pódense consultar seleccionando a provincia correspondente. Selecciona a túa provincia:
- Se necesitas datos de anos anteriores ou de máis indicadores podes consultalos directamente nas táboas de indicadores de mortalidade e de indicadores de poboación.
Descarga da ficha en pdf 
Índice
- Indicadores demográficos
- ¿Existe algunha relación entre a taxa bruta de mortalidade e o índice de envellecemento?
- ¿Existe algunha forma de resumir numéricamente a información contida no gráfico de dispersión?
- ¿Que medida da relación lineal entre dúas variables non depende das unidades de medida?
- ¿Como axustamos a recta de regresión?
- ¿Como predecir valores da variable coa recta de regresión?
Indicadores demográficos
Os indicadores demográficos proporcionan a información necesaria para o estudo da estrutura e
evolución dunha poboación e permiten facer comparacións temporais ou entre distintos ámbitos xeográficos.
Na Táboa 1 móstranse os datos do índice de envellecemento e da taxa bruta de mortalidade para os concellos da provincia de Lugo no ano 2023 (excepto Negueira de Muñiz).
Táboa 1: Taxa bruta de mortalidade e índice de envellecemento nos concellos da provincia de Lugo
¿Existe algún tipo de relación entre as variables "Taxa de mortalidade" e "Índice de envellecemento"? 
O primeiro paso é representar graficamente os datos. Empregaremos o "diagrama de dispersión" ou "nube de puntos", que permite representar nos eixos coordenados os pares de puntos formados polos valores observados de ambas as dúas variables.
Este tipo de representación gráfica permite apreciar a existencia e o tipo de relación existente entre ambas as dúas variables.
¿Que variable escollemos para cada eixo?
No eixo de ordenadas representamos a variable explicada (tamén chamada endóxena ou dependente) e no eixo de abscisas a variable explicativa (esóxena ou independente).
Parece lóxico pensar que a taxa bruta de mortalidade de cada concello depende do índice de envellecemento así que, neste caso a variable explicada é a taxa bruta de mortalidade e a variable explicativa é o índice de envellecemento.
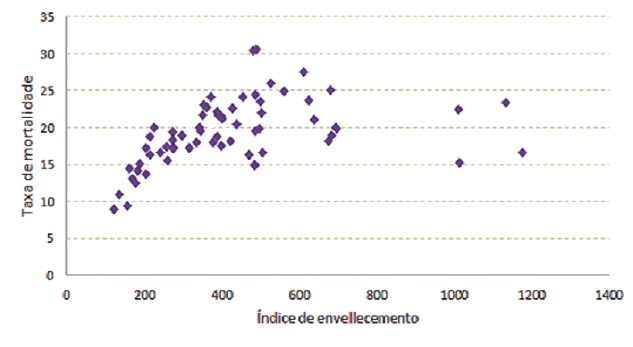
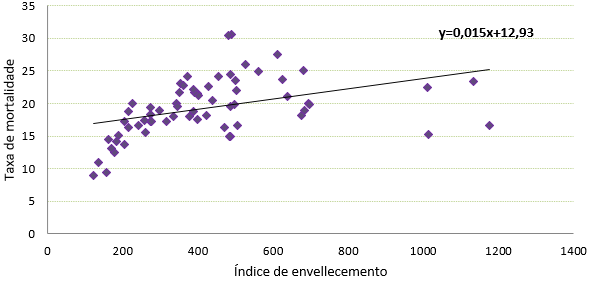
Obtense o seguinte gráfico de dispersión:
+ Como elaborar un gráfico de dispersión coa folla de cálculo OpenOffice Calc (Video demostración)
¿Que conclusión podemos deducir do gráfico de dispersión?
Ao observar o gráfico pódese apreciar que ao aumentar os valores da variable independente (representada no eixo das X), aumenta en promedio o valor da variable dependente (representada no eixo das Y). Cando esto ocorre dicimos que existe unha relación positiva ou directa entre ambas as dúas variables. Efectivamente, o gráfico mostra que os concellos con alto índice de envellecemento tenden a ter tamén unha elevada taxa bruta de mortalidade, confirmando así o que sospeitabamos.
Pero a figura tamén parece amosar algo máis. Se lle botas un pouco de imaxinación poderás ver como os puntos parece que tenden a colocarse seguindo unha recta. Dicimos entón que a relación entre ambas as dúas variables é lineal. Esta relación é de tipo estatístico, é dicir, os puntos distribúense "aleatoriamente" arredor da recta.
Se a relación fose funcional (y= a + bx), non necesitarías botarlle nada de imaxinación, pois os puntos formarían unha recta perfecta.
¿Existe algunha forma de resumir numericamente a información contida no gráfico de dispersión? 
¡A covarianza! Esta medida dá información sobre a asociación lineal entre dúas variables. !Coidado! Mide a asociación lineal pero non proporciona ningunha información se a relación é doutro tipo.
No noso caso temos:
A covarianza é distinta de 0, polo que podemos dicir en principio que hai certa dependencia lineal. Ademais, esta é positiva xa que o signo da covarianza tamén o é.
¿Poderiamos a partir da covarianza dicir se a relación é forte ou débil?
Non. A covarianza non é unha medida adimensional, depende das unidades de medida, non ten un valor máximo polo que non hai uns límites a partir dos que se poida considerar que a dependencia lineal sexa máis forte.
¿Que medida da relación lineal entre dúas variables non depende das unidades de medida? 
Para construír unha medida da relación lineal entre dúas variables, que resuma a información do gráfico de dispersión e que non dependa das unidades de medida, a solución proposta por Galton e Pearson foi tipificar a covarianza dividíndoa polas desviacións típicas de ambas as dúas variables. O resultado chámase coeficiente de correlación lineal de Pearson. Para os datos deste exemplo o seu valor é o seguinte:
O coeficiente de correlación é un número comprendido entre -1 e 1.
- Se o coeficiente de correlación lineal toma valores cercanos a -1 a correlación é forte e inversa, e será tanto máis forte canto máis se aproxime r a -1.
- Se o coeficiente de correlación lineal toma valores cercanos a 1 a correlación é forte e directa, e será tanto máis forte canto máis se aproxime r a 1.
- Se o coeficiente de correlación lineal é igual a 0 non existe relación lineal pero podería existir unha relación moi forte entre as dúas variables pero de tipo non lineal.
- Se r = 1 ó -1, os puntos da nube están sobre a recta crecente ou decrecente. Entre ambas as dúas variables hai dependencia funcional.
Neste exemplo o coeficiente de correlación é 0,40 polo tanto estamos nun caso de relación lineal positiva.
¿Como axustamos a recta de regresión? 
O valor do coeficiente de relación lineal indica unha relación lineal relativamente forte, polo que pódese tratar de axustar a recta de regresión á nube de puntos. A recta de regresión é a recta que describe como varía a media da variable dependente en función da independente.
A ecuación dunha recta é da forma y= a + bx. Trátase agora de atopar os coeficientes a e b.
Os valores dos parámetros a e b, obtidos mediante o método de mínimos cadrados teñen a seguinte expresión:
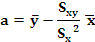
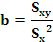
Cos datos do exemplo:
e, polo tanto, a expresión da recta de regresión é y = 12,93 + 0,015 x
No seguinte gráfico representamos a recta de regresión xunto co diagrama de dispersión.
"Xogando a ser Nostradamus" ou "¿como utilizar a recta de regresión para predicir?"
Supoñamos que non coñecemos a taxa bruta de mortalidade do concello de Taboada, pero que si temos información sobre o seu índice de envellecemento. ¿Como poderiamos facer para predicir (estimar) o valor da taxa bruta de mortalidade?
A ecuación da recta de regresión relaciona ambas as dúas variables (o índice de envellecemento e a taxa bruta de mortalidade). Coñecemos o valor do índice de envellecemento do concello de Taboada. ¿Podemos entón obter o valor da taxa bruta de mortalidade a partir da recta?
¡Claro que si! Na recta, coñecido o valor de x (índice de envellecemento) o valor da y (taxa bruta de mortalidade) que lle correspondería sería y = 12,93 + 0,015 x. Logo, substituíndo:
y= 12,93+ 0,015 x 482,1 = 20,16
¿Cal é o residuo ou erro de predición cometido ao utilizar a recta de regresión?
erro de predición=valor observado-valor esperado
Neste caso, o erro de predición sería entón: e = 20,16- 30,46 =-10,30.
No gráfico que representa a recta de regresión sobre a nube de puntos hai algúns deles que quedan bastante alonxados da recta. Nestes casos a predición dada pola recta de regresión (que é o valor da y no corte da recta coa perpendicular ao eixo de abscisas dende o punto en cuestión) non sería moi boa.
Podes calcular os erros de predición cometidos nos concellos de Cervantes (e = -6,54) e de Burela (e=-5,82).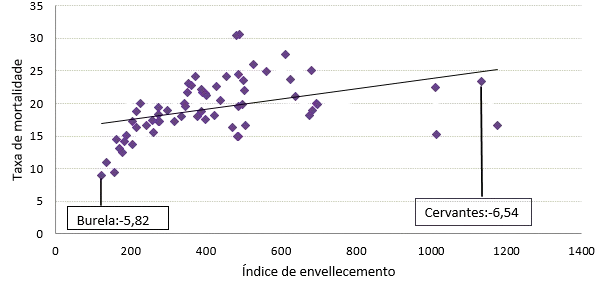
A estimación loxicamente é mellor canto máis próximos á recta se atopen os puntos do diagrama de dispersión.
Se non tivésemos a taxa bruta de mortalidade dalgúns concellos pero si o índice de envellecemento. ¿Como fariamos?. Estimariamos a recta de regresión usando só os concellos con información completa, e utilizariamos esta recta así construída para predicir a variable independente (taxa bruta de mortalidade) naqueles nos que só coñecemos o valor da variable dependente (índice de envellecemento).
Esta recta construída sen empregar todos os concellos, será máis ou menos parecida á nosa dependendo do concello que quite.
Podes contestar ás preguntas formuladas na actividade cos datos da túa provincia e cos de toda Galicia, que podes atopar na ligazón que aparece ao principio desta páxina.
Ademais, podes elixir un concello e construír a recta de regresión sen utilizar ese concello:
- Obtén a estimación da taxa bruta de mortalidade do dito concello usando esa recta.
- Compara o resultado co valor real da taxa bruta de mortalidade para o dito concello.
